CS231n笔记｜3 损失函数和最优化

3 损失函数和最优化（loss Function and optimization）

损失函数（SVM、Softmax）、正则化、最优化（梯度计算、梯度下降-BGD\\SGD\\MBGD）、图像的特征表示

3.1 损失函数

损失函数衡量线性分类器W：要写一个算法可以自动决定哪些W是最优的，可以用一个函数把W当做输入，然后观察得分，定量地衡量任意一个W的好坏，这个函数就称为损失函数。如果对训练数据进行分类方面表现不佳，那么损失就会很高，如果好的话，就会很低。从W的可行域里，有效地找到W取何值才是最小化损失函数（最好的情况），这就是优化过程。

下图是分类器对三张测试图的评分，对汽车的分类效果最好，分类的评分中汽车类得分最高，而猫和青蛙的得分在当中并不是最高的，分类错了。

有些训练数据集x和y，N个样本中x是算法的输入，x是图片的每个像素点，y就是算法想要预测的东西（也叫标签或目标），把CIFAR-10中的每个图片分类到10个类中的一个，所以标签y就是1~10间的整数，这个整数可表明对每个图片x哪个类是正确的。

损失函数记为Li，预测函数f通过样本x和权重矩阵W，给出预测分数或者说标签y，Li可以定量地描述训练样本预测的好不好，最终的损失函数L是在整个数据集中N个样本的损失函数的总和的平均。找到在训练集上使损失函数最小化的W即可。

3.1.1 SVM损失函数

二元SVM（支持向量机）中只有两个类，每个样本x被分为正例或负例。多类支持向量机（SVM）损失这个损失就是在说如果真实分类的分数比其他的分数高出一个安全边距以上时，结果才会满意，否则会有一些损失，损失越低越好。

1.计算SVM损失函数

计算解释：对单个样本的多类SVM损失函数Li，除了真实的分类yi以外，对所有的分类y都做加和，在所有错误的分类上做和，比较正确分类的分数和错误分类的分数，如果正确分类的分数比错误分类的分数高出某个安全的边距，这个边距为1，或者真实的分数很高，比其他任何错误分类的分数都高很多，那么损失为0，然后把图片对每个错误分类的损失加起来，就可以得到这个样本的最终损失，最后对整个训练集的不同样本的损失函数取平均值得到整个损失L。

公式注释：s是分类器预测出来的分数s=f(xi,W)，整数yi表示某个样本的正确的分类标签，s_yi代表了训练集的第i个样本的真实分类的分数。如果s_j - s_yi + 1<=0则使其为0，否则为s_j - s_yi + 1，即选两者的最大值。

如下为计算的单个训练样本的SVM损失Li和整个数据集的SVM损失L。L=5.27衡量了此分类器在数据集上的效果很差。

2.折页损失

这种某个值和0取max的损失函数，也可以称为折页损失（Hinge loss）函数，因为可用下图表示，x轴是s_yi训练样本真实分类的分数，y轴是损失，随着真实分类的分数提升，损失会线性下降，一旦分数超过了一个阈值，损失函数就是0，因为已经为这个样本成功地分对了类。

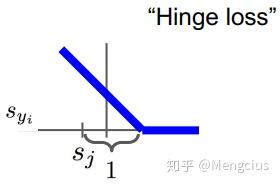
3.问题解答

SVM损失函数只会关注于正确分数比错误分数是否大过了1，汽车的分数如果变化了一点点，不会超过1的界限，损失函数不会改变依然是0。

SVM损失函数最小值是0，最大值是无穷大，参看合页损失函数示图。

在初始化参数时，并从头训练，通常先用一些很小的随机值来时初始化w，那么分数在训练初期倾向于呈现均匀较小的值。如果所有的分数s近乎为0时，损失函数大约为1。在实际调试时，刚开始训练时不为1，那就可能有个BUG。

在公式max上加一个平方项，会变成非线性的另一种损失函数，在实际中有应用。平方会使错误严重化；线性对微小错误不在意，如果出现很多错误就扩大错误，以此来减小它。

对SVM所有错误的分数求和，将所有正确的求和，将所有的都求和，损失函数会增加1。（疑问？）

对SVM所有的求平均值，损失函数不会改变，所以当选择数据集时分类的数量要提前选定，因为这只是将损失函数缩小了一个倍数，缩放操作不会有影响。（疑问？）

4.程序

在numpy库中实现损失函数（没有正则化），有非向量化和半向量化形式，只迭代一个类而不是所有，只是把想要跳过的那个清零，然后计算总和：

def L_i(x, y, W):
"""
unvectorized version. Compute the multiclass svm loss for a single example (x,y)
- x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
with an appended bias dimension in the 3073-rd position (i.e. bias trick)
- y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
- W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
"""
delta = 1.0 # see notes about delta later in this section
scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
correct_class_score = scores[y]
D = W.shape[0] # number of classes, e.g. 10
loss_i = 0.0
for j in xrange(D): # iterate over all wrong classes
if j == y:
# skip for the true class to only loop over incorrect classes
continue
# accumulate loss for the i-th example
loss_i += max(0, scores[j] - correct_class_score + delta)
return loss_i


def L_i_vectorized(x, y, W):
"""
A faster half-vectorized implementation. half-vectorized
refers to the fact that for a single example the implementation contains
no for loops, but there is still one loop over the examples (outside this function)
"""
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y]- scores[y]canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_i


def L(X, y, W):
"""
fully-vectorized implementation :
- X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
- y is array of integers specifying correct class (e.g. 50,000-D array)
- W are weights (e.g. 10 x 3073)
"""
# evaluate loss over all examples in X without using any for loops
# left as exercise to reader in the assignment

假设我们找到了一个W，使得损失值L=0，这个W不是唯一的，加倍W也能使L=0。这是因为加倍W，正确与不正确的安全边界值也会翻倍，所以损失函数值依然为0。

5.正则化

正则化（Regularization）的宏观概念就是要对模型做的任何事，也就是惩罚，主要目的是为了减轻模型的复杂度，而不是试图拟合数据，减少泛化误差，而不是减少训练误差。

如果让分类器尝试和适应训练数据，就会非常拟合，完美分类所有的训练数据点。这样并不好，我们关心的是测试数据的性能，适合新的数据，这在机器学习里的通常解决方式就是正则化概念，所以除了需要高数分类器拟合训练集外，还要为损失函数添加一个正则项，鼓励模型以某种方式选择更简单是W，以得到下图中的绿线，这里的简单取决于任务的规模和模型的种类。

设正则化惩罚项（regularization penalty）为R，损失函数有两个项，数据损失项和正则项，用超参数λ平衡这两个项。。如果λ越大，权重W就会被惩罚的越多，W数值越小，这样算出来的分数越小，概率的分布越分散，最终接近均匀分布。

正则化类型：最常用的正则化惩罚是L2正则化（权值衰减），L2范式通过对所有参数进行逐元素的平方惩罚来抑制大数值的权重；L1正则化有很好的性质像在这个矩阵W中鼓励稀疏。弹性网络正则化是L1和L2的组合；最大规范正则化的惩罚是最高准则而不是L1或L2准则；其他正则化类型如脱网（Dropout）、批量归一化，随机深度。

L2正则化如何度量复杂性的模型？在线性分类的情况下，w1和w2其实是一样的，因为他们与x点乘的计算结果一样，但是w2的L2回归性更好一点，因为他有较小的范数。线性分类器中wi反应的是x对输出的影响程度，所以L2正则化的作用是它更能传递出x中不同元素值的影响，当输入的xi存在变化时它的鲁棒性可能更好，判断时主要取决于x的整体情况，而不是特定元素。L1正则化相反，更倾向于w1，L1的度量复杂性的方式可能是非零元素的个数，而L2更多考虑W整体分布。

添加正则化不会改变线性分类器的工作方式，像是多项式回归的例子，参数W就是多项式f(x)=0+x+x^2+x^3+...的系数，对W惩罚就是让f(x)向低阶多项式演进，减轻复杂度。

3.1.2 Softmax损失函数

Softmax分类器 (多元逻辑回归，Multinomial Logistic Regression)这个损失函数在深度学习里使用更广泛。

1.计算Softmax函数

用Softmax函数将分数指数化以便结果都是正数，再用这些指数的和来归一化它们，就有了各类的0~1间的概率分布，所有类别的概率和等于1。这是从分数推导出来的概率分布，拿他同目标值或者说真实的概率分布进行比较，如果知道是猫时，目标的概率分布应该把所有的概率集中在猫上面，猫的概率是1，其他是0。现在我们要促使通过Softmax计算的概率分布取去匹配上述的目标概率，即正确的类别应该具有几乎所有的概率。

可以有多种方式列这个方程，如在目标概率分布与计算出的概率分布间计算KL散度，比较它们差异，用最大似然估计。真实类别的概率比较高并趋近于1，损失函数就是真实类别概率的对数再取负数，这个log函数是一个单调函数，找Log的最大值相对容易，又因为损失函数是度量坏的程度，所以加了负号。用Softmax对分数进行转化处理，并得到正确类别的损失函数是-log P。

求Softmax损失函数的实例：分数 - 指数化 - 归一化 - -log。

2.问题解答

Softmax损失函数的最小值是0，最大值是无穷大。想要正确类别概率是1，不正确类别概率是0，1的对数是0，1的对数的负值是0，损失值就是0，这种情况理论上只有为正确分类取一个无穷大的分值，为所有不正确的分类取负无穷大的分值。

如果所有的s都很小近乎为0，损失值是log(C)。

交叉熵损失函数“想要”预测分布的所有概率密度都在正确分类上。

3.Softmax比较SVM

（1）SVM和Softmax损失函数两者在线性分类方面一样，得到分值向量后，两个损失函数的区别是如何理解这些分值，进而度量好坏。不同之处在于对f中分值的解释：SVM分类?将它们看做是分类评分，它的损失函数鼓励正确分类（本例蓝色）的分值比其他分类的分值高出至少一个边界值。 Softmax分类?将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。

（2）假设拿了一个数据点稍微改变了它的分数， SVM关心的是正确的分值比不正确的分值至少高出一个安全边界，SVM更加局部目标化，对数字个体的细节不关心：如果分数是[10, -100, -100]或者[10, 9, 9]，对于SVM来说没什么不同，只要满足超过边界值等于1，那么损失值就等于0； Softmax的目标是将正确分类的概率质量等于1。softmax分类?对于分数是永远不满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小，从而在正确分类上积累更多的概率质量。

SVM得到这个数据点超过阈值，要正确分类，然后放弃这个数据点；Softmax总是试图不断提高，每个数据点都会越来越好。两者理解有差别，到应用结果差别不大。

（3） SVM的计算是无标定的，而且难以针对所有分类的评分值给出直观解释。Softmax分类?允许我们计算出对于所有分类标签的可能性。SVM分类?可能给你的是一个[12.5, 0.6, -23.0]对应分类猫、狗、船。而softmax分类?可以计算出这三个标签的”可能性“是[0.9, 0.09, 0.01]，这就让你能看出对于不同分类准确性的把握。可能性分布的集中或离散程度是由正则化参数λ直接决定的，λ是可以直接控制的一个输入参数。如果λ越大，权重W就会被惩罚的越多，W数值越小，这样算出来的分数越小，概率的分布越分散，最终接近均匀分布。如下图λ变大，分数变小时，softmax函数计算出的概率分散了：

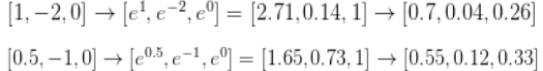
4.损失函数可视化

损失函数一般都是定义在高维度的空间中（比如在CIFAR-10中一个线性分类?的权重矩阵大小是[10x3073]，就有30730个参数），要将其可视化就很困难。但可以在1个维度或者2个维度的方向上对高维空间进行切片来感受。例如随机生成一个权重矩阵 ，该矩阵就与高维空间中的一个点对应。然后沿着某个维度方向前进的同时记录损失函数值的变化。用在两个维度上，通过改变a、b来计算损失值L(W+aW1+bW2)，从而给出二维的图像。在图像中a、b可以分别用x和y轴表示，而损失函数的值可以用颜色变化表示。

一个无正则化的多类SVM的损失函数的图示如下。左边和中间只有一个样本数据，右边是CIFAR-10中的100个数据。左：a值变化在某个维度方向上对应的的损失值变化。中和右：两个维度方向上的损失值切片图，中间蓝色部分是低损失值区域，边缘红色部分是高损失值区域。注意损失函数的分段线性结构。多个样本的损失值是总体的平均值，所以右边的碗状结构是很多的分段线性结构的平均（比如中间这个就是其中之一）。

从一个维度方向上对数据损失值的展示如下。x轴方向就是一个权重，y轴就是损失值。数据损失是多个部分组合而成。其中每个部分要么是某个权重的独立部分，要么是该权重的线性函数与0阈值的比较（由公式中max可知）。完整的SVM数据损失就是这个形状的30730维版本。

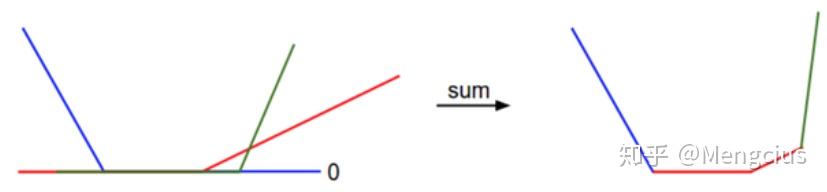
根据SVM的损失函数的碗状外观猜出它是一个凸函数。关于如何高效地最小化凸函数的论文有很多，你也可以学习斯坦福大学关于（凸函数最优化）的课程。但是一旦我们将f函数扩展到神经网络，目标函数就就不再是凸函数了，图像也不会像上面那样是个碗状，而是凹凸不平的复杂地形形状。

注意由于max操作，损失函数中存在一些不可导点，使得损失函数不可微，梯度是没有定义的，但是次梯度（subgradient）依然存在且常常被使用。

3.2 最优化

最优化（Optimization）是寻找能使得损失函数值最小化的参数W的过程。而损失函数可以量化某个具体权重集W的质量。图像分类任务中的三个关键部分有评分函数、损失函数和最优化。一旦理解了这三个部分是如何相互运作的，我们将会回到第一个部分（基于参数的函数映射），然后将其拓展为一个远比线性函数复杂的函数：首先是神经网络，然后是卷积神经网络。而损失函数和最优化过程这两个部分将会保持相对稳定。

1.最优化方案

（1）随机搜索

寻找最好的权重W就好比找权重空间中山谷的底部。最笨的方法是随机搜索，随机采样很多权重值，将它们输入损失函数，观察效果。 它的核心思想是迭代优化，在一个权重矩阵集中随机选择一个权重W，然后迭代取优， 每次都让它的损失值变得更小一点，从而获得更低的损失值。

随机生成若干权重矩阵W，取出最好的权重W：

# 假设X_train的每一列都是一个数据样本（比如CIFAR-10的3073 x 50000）
# 假设Y_train是数据样本的类别标签（比如一个长50000的一维数组）
# 假设函数L()对损失函数进行评价
bestloss = float("inf") # Python分配最高可能的浮点值。
for num in xrange(1000):
    W = np.random.randn(10, 3073) * 0.0001 # 生成随机参数（或者在权重矩阵集中随机选择）
    loss = L(X_train, Y_train, W) # 获得整个训练集的损失
    if loss < bestloss: # 保持最佳结果
        bestloss = loss
        bestW = W
    print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)
# 输 出:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# ... (trunctated: continues for 1000 lines)

用上面最好的权重W跑测试集，算出准确率：

# 假设X_test尺寸是[3073 x 10000], Y_test尺寸是[10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, 所有测试样本的分类分数
# 找到在每列中评分值最大的索引（即预测的分类）
Yte_predict = np.argmax(scores, axis = 0)
# 以及计算准确率
np.mean(Yte_predict == Yte)
# 返回 0.1555 

可以用这种随机搜索训练一个线性分类器，对CIFAR-10来说有10个类别随机概率就是10%，通过几次随机试验，会得到W值的设定使精确度达到15%，但效果很查不能用。

（2）随机本地搜索

每走一步都尝试几个随机方向，如果某个方向使损失减少，就向该方向走一步。从一个随机W开始，然后生成一个随机的扰动δW，只有当W+δW的损失值变低，才会更新。这个过程的代码如下：

W = np.random.randn(10, 3073) * 0.001 # 生成随机初始W
bestloss = float("inf")
for i in xrange(1000):
    step_size = 0.0001
    Wtry = W + np.random.randn(10, 3073) * step_size
    loss = L(Xtr_cols, Ytr, Wtry)
    if loss < bestloss:
        W = Wtry
        bestloss = loss
    print 'iter %d loss is %f' % (i, bestloss)

使用同样的数据（测试1000），这个方法可以得到21.4%的分类准确率。这个比策略一好，但是依然过于浪费计算资源。

（3）跟随梯度

前两个策略中，是在权重空间中找到一个方向，沿着该方向能降低损失函数的损失值。其实不需要随机寻找方向，可以直接计算出最陡峭的方向，沿着斜坡走，这个方向就是损失函数的梯度。这正是我们训练神经网络、线性分类器时普遍使用的方法。

一维函数中，x为标量，输出为曲线的高度，斜率就是函数在某一点的瞬时变化率，一维中叫导数，根据极限定义可求出导数。

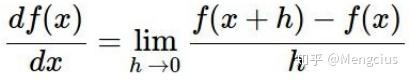
多维中，x可能是整个向量，在多元情况下生成的导数就叫偏导数，梯度（gradient）就是各个维度的偏导数组成的向量，梯度中每个元素可以告诉相关方向上函数f的斜率。某点任意方向的坡度就等于这点上梯度和该点单位方向向量的点积，梯度指向函数增加最快的方向，负梯度指向函数下降最快的方向。梯度给出了函数在当前点的一阶线性逼近，所以很多深度学习中都是在计算函数的梯度，然后用这些梯度迭代更新参数向量。

2.梯度计算方法

（1）有限差值数值计算法

计算梯度的一个简单方法是使用有限差值进行数值计算，梯度dW和权重W的维数相同，dW中的每个元素都告诉我们在相关方向上每移动一小步损失变化多少。根据导数定义计算有限差分时，只将W的第一个元素累加一个很小的值h，然后用损失函数重新计算损失值，用损失值之差除以h既得到dW，向负梯度方向移动一个步长。如第一维做微小改变h后，损失值将从1.25347降低到1.25322，计算得到dW，在梯度的第一维实现有限差分逼近；第二维种重新将第一维的值恢复为原值，重复相同操作，在第二维方向上增加一小步，计算损失，使用有限差分逼近，在第二维计算出梯度的近似值；第三维等重复。

计算数值梯度的复杂性和参数的量线性相关，在CIFAR-10中一个线性分类?

的有30730个权重参数，所以损失函数每走一步就需要计算30731次损失函数的梯度。如卷积神经网络非常大，耗费计算资源太多，非常慢，h值是近似值效果也不好，常用来检验梯度。

计算函数f在点x处的梯度的通用函数：（根据导数公式和有限差分法得来）

def eval_numerical_gradient(f, x):
    """
    一个f在x处的数值梯度法的简单实现
    - f是只有一个参数的函数
    - x是计算梯度的点
    """
    fx = f(x) # 在原点计算函数值
    grad = np.zeros(x.shape)
    h = 0.00001
    # 对x中所有的索引进行迭代
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        # 计算x+h处的函数值
        ix = it.multi_index
        old_value = x[ix]
        x[ix] = old_value + h # 增加h
        fxh = f(x) # 计算f(x + h)
        x[ix] = old_value # 存到前一个值中 (非常重要)
        # 计算偏导数
 grad[ix] = (fxh - fx) / h # 梯度
        it.iternext() # 到下个维度
    return grad

用上面的公式求CIFAR-10损失函数的梯度：（f即L，x即W）

# 要使用上面的代码我们需要只有一个参数的函数
# (在这里参数就是权重)所以也包含了X_train和Y_train
def CIFAR10_loss_fun(W):
    return L(X_train, Y_train, W)
W = np.random.rand(10, 3073) * 0.001 # 随机权重向量
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # 得到梯度

W位置更新，负梯度乘以步长：

loss_original = CIFAR10_loss_fun(W) # 初始损失值
print 'original loss: %f' % (loss_original, )
# 查看不同步长的效果
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
    step_size = 10 ** step_size_log
 W_new = W - step_size * df # 权重空间中的新位置
    loss_new = CIFAR10_loss_fun(W_new)
    print 'for step size %f new loss: %f' % (step_size, loss_new)
# 输出:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652  步长过大越多最低点
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802  最低点
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036  步长小进展慢

为了计算W_new，要向着梯度df的负方向去更新，这是因为我们希望损失函数值是降低而不是升高。

步长（也叫作学习率）将会是神经网络训练中最重要（最头痛）的超参数之一，代表每次计算梯度时，在那个方向前进多少距离，因倾斜程度不同，该跨出的步长是不确定，小步长下降稳定但进度慢，大步长进展快但是风险更大，可能导致错过最优点，让损失值上升。在训练网络时要先确定合适的步长，然后再说模型大小、需要多少正则化等。

（2）微分分析梯度法

直接用微积分（Calculus）分析，计算出梯度的表达式（不是近似的），计算速度很快，但实现时容易出错。

SVM损失函数，右上角T表矩阵转置：

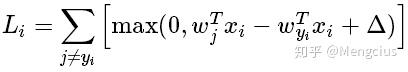
例如直接让SVM损失函数对W_yi进行微分得到梯度：

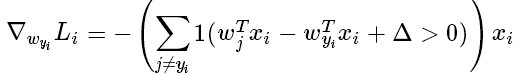
括号中的条件为真，那么函数值为1，如果为假，则函数值为0。代码实现的时候比较简单：只需要计算没有满足边界值的分类的数量，然后乘以xi就是梯度了。

注意，这个梯度只是对应正确分类的W的行向量的梯度，那些j不等于yi行的梯度是：

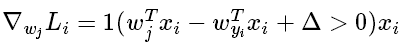
两方法比较：

数值梯度（Numerical gradient）：近似，缓慢，易于写，用来检验梯度。

分析梯度（Analytic gradient）：精确，快速，容易出错，用来计算梯度。

在实际操作时用分析梯度来计算梯度值，再将数值梯度法的结果作比较检查，这叫做梯度检查。用数值梯度作为单元测试，来确保解析梯度是正确的。

3.梯度下降方法

程序重复地计算梯度然后对权重参数进行更新，这一过程称为梯度下降。梯度下降计算量巨大，是最为复杂的深度学习算法的核心，初试化W为随机值，当为真时，计算损失和梯度，然后向梯度相反方向更新权重值，所以一直向函数最大减小方向前进一小步，最后网络会收敛， 结果不再变化。梯度下降是对神经网络的损失函数最优化中最常用的方法。

梯度下降的方法有三种：批量梯度下降法BGD、随机梯度下降法SGD、小批量梯度下降法MBGD。如果样本量比较小，采用批量梯度下降算法；如果样本太大，或者在线算法，使用随机梯度下降算法；在实际的一般情况下，采用小批量梯度下降算法。

（1）批量梯度下降法

批量梯度下降法（Batch Gradient Descent，BGD）是梯度下降法最原始的形式，在更新每一参数时都使用所有的样本来进行更新，m表示样本的所有个数。当f(x)是凸函数的时候，用批量梯度下降的方法取得的最小值是全局最优解，但需要在每一步计算梯度，每更新一个参数都要遍历完整的训练集。

优点：全局最优解，易于并行实现，样本小时使用；

缺点：当样本数目很多时，训练过程会很慢。

# 批量梯度下降
while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += - step_size * weights_grad # 进行梯度更新

（2）随机梯度下降法

随机梯度下降（Stochastic Gradient Descent，SGD）在每一次更新参数时都使用一个样本来进行更新，m等于1，更新很多次，有时候也被称为在线梯度下降。当样本数据很大时，可能到迭代完成，也只不过遍历了样本中的一小部分。因此其速度较快，但最终的结果是在全局最优解的附近。对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次，这种跟新方式计算复杂度太高。

SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。即使SGD在技术上是指每次使用1个数据来计算梯度，还是会有人使用SGD来指代小批量数据梯度下降。

优点：训练速度快，样本太大时使用；

缺点：准确度下降，并不是全局最优，不易于并行实现，迭代次数多。

其代码段简单在训练样本下的增加了一个循环，计算出对于每个样本下的梯度，每次epoch都shuffle了训练集。

# 随机梯度下降
for i in range(nb_epochs):
 np.random.shuffle(data) 
 for example in data: #这的data换成get_batches(data, batch_size=50)就是MBGD
        params_grad = evaluate_gradient(loss_function, example,params)                
        params = params - learning_rate * params_grad

（3）小批量梯度下降法

小批量梯度下降（Mini-batch Gradient Descent，MBGD）是在更新每一参数时都使用一部分样本来进行更新权重，m的值大于1小于所有样本的数量。这是因为训练集中的数据都是相关的，小批量数据的梯度可以近似整个数据集梯度。因此在实践中通过计算小批量数据的梯度可以实现更快速地收敛，并以此来进行更频繁的参数更新。它克服上面两种方法的缺点，又同时兼顾两种方法的优点，一般情况下使用他。

例如，在目前最高水平的卷积神经网络中，一个典型的小批量包含256个例子，用来实现一个权重参数更新。程序另一种写法。

# 普通的小批量数据梯度下降
while True:
    data_batch = sample_training_data(data, 256) # 256个数据
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weights += - step_size * weights_grad # 参数更新

小批量数据的大小是一个超参数，但是一般并不需要通过交叉验证来调参。它一般由存储?的限制来决定的，或者干脆设置为同样大小，比如32，64，128等2的指数，这样运算更快。

最优化过程图示：如下图表示损失函数，线条表示最优化过程，中间红色部分表示损失值较低，边缘蓝色和绿色代表较高的误差值。从某个随机点W，开始计算梯度的反方向（白箭头方向是负梯度方向），我们希望它指向最终的最小值，黑线参数朝着中心点迂回前进，不断逼近最小值。下图中蓝线和红线基于利用每一步的梯度决定下一步方向的基本算法，运用了更高级的迭代规则，有不同的更新策略来决定如何使用梯度信息，这两种方法是带动量的梯度下降、Adam优化器。

4.交互式的网页Demo

直观地理解线性分类?：使用梯度下降来训练线性分类器，调节W会导致决策区域边界进行旋转，改变偏差值b导致决策区域边界平行向上或向下移动，可以调整步长，可以调整损失函数。http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/

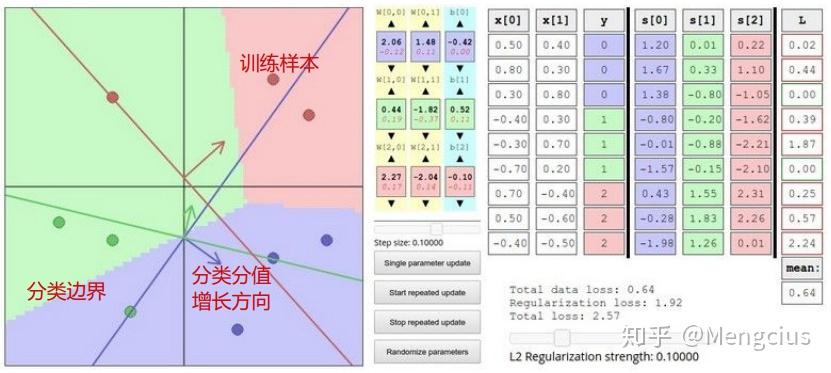
5.总结

1）有了xi和yi数据集，用基于参数的评分函数将原始图像像素映射为不同类别的分类评分值，如一个线性分类器，用x计算出评分s（或f）。

2）然后用损失函数（SVM、Softmax等）比较分类评分和训练集图像数据实际分类是否一致，来衡量算法分类预测的质量。损失函数包含数据损失和正则项，数据损失计算的是分类评分f和实际标签y之间的差异，正则项只是一个关于权重的函数，使其减少泛化误差，趋向更简单的模型。

3）最优化更新W使损失最小，用梯度下降方法重复计算权重的梯度，实现权重参数的更新。最终可得到分类效果更好的分类器。

3.3 图像的特征表示

因为多模态等原因，如果直接输入原始像素值给线性分类器，表现并不好。所以在深度神经网络大规模应用前，分两步，首先计算图片的各种代表特征，如计算与图片形象有关的数值，然后将不同的特征向量合到一起，得到图像的特征描述，它将作为输入源传入线性分类器。

动机：如下训练数据集，不能用一个线性的决策边界分开，但如果用灵活的特征转换，如将其极坐标转换就可以线性分开了。在图像中用图像特征表示可能效果更好。

1.颜色直方图

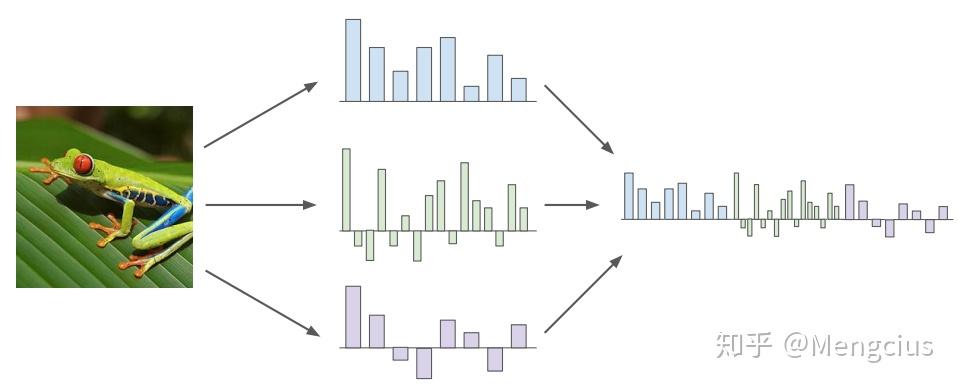
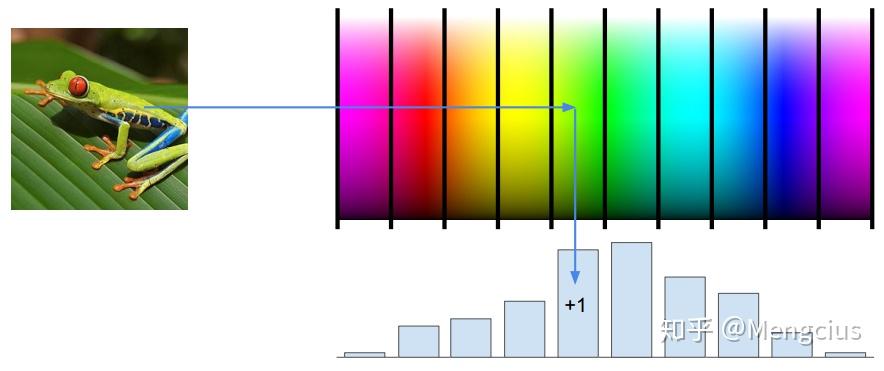
特征表示的简单例子就是颜色直方图，按照每个像素值对应的光谱，将每个像素都映射到下面柱状里，然后计算出柱状里像素点出现的频次。如下特征向量表示有很多的绿色向量。

2.方向梯度直方图

在神经网络兴起前就是一个常用的特征向量就是方向梯度直方图。步骤如先获取小图像，将图像按8个像素区分为8份，然后在8个像素区的每个部分计算像素值主要的边缘方向，把这些边缘方向量化到几个组，然后每个区域内得到一个直方图。现在全特征向量就是这些不同组的边缘方向直方图，这个直方图是从图像的8个区域得来的。

如下图将图像划分为每个区域内有8x8像素，将边缘方向量化为9个像素，320x240图像被划分为40x30个bins，在每个bins中有9个数字，因此特征向量有30*40*9=10800个数字。图中的边缘就是获取的方向梯度特征表示的直方图。

3.词袋

另一个特征表示的例子就是词袋（Bag of Words），这是从自然语言处理中来的灵感，用一个特征向量表示这段话的方法是计算不同词在这段话中出现的次数。它有两步，第一步获得一堆图像，从这些图像中进行小的随机块的采样，然后用K均值将它们聚合成簇，从而得到不同的簇中心，这些簇中心可能代表了图像中视觉单词的不同类型。如下图聚类后视觉单词获取了不同颜色，就像不同方向有向边缘的不同类型，数据驱动方式下，从数据中获得这些有向边缘。

第二步一旦获得一系列视觉单词成为码本，就可以利用这些视觉单词来给图像编码，这个视觉单词会在图像中出现多少次呢。这种特征表示给了我们关于图像视觉外观的信息。

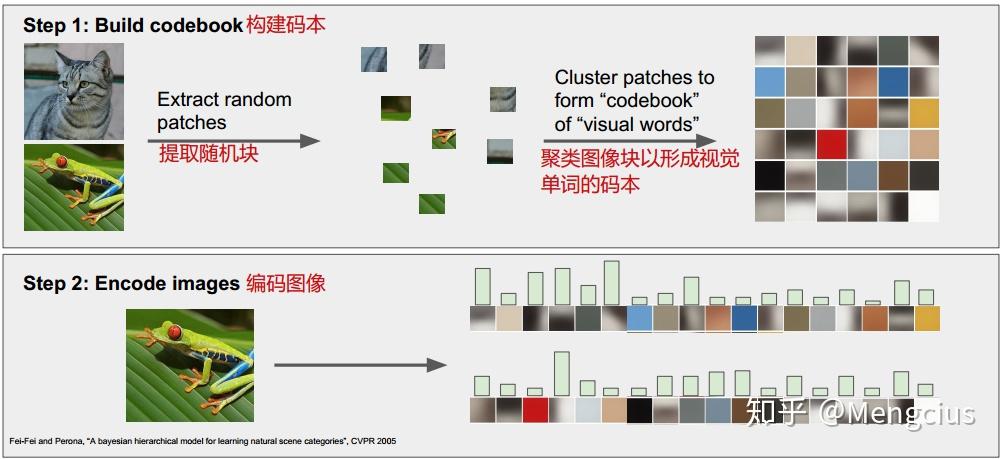
选自论文Fei-Fei and Perona, “A bayesian hierarchical model for learning natural scene categories”, CVPR 2005。

4.图像特征比较神经网络

计算图像不同特征表示的差异，如词袋、方向梯度直方图将整个特征连接在一起，来喂养这些线性分类器的特征提取器，这种更复杂一点但更常见。在提取这些特征之后，固定特征提取器使它在训练中不会被更新，而在训练中如果它用于更重要的特征的话仅仅更新线性分类器。

卷积神经网络和这些深度神经网络和上面的没什么区别，唯一的差别就是并非提前记录特征，而是直接从数据中学习特征，所以将像素值输入卷积神经网络，经过多层计算，最终得到一些数据驱动的特征表示的类型，然后在整个网络中训练所有的权重，而不是最上层的线性分类器的权重。接下来引入神经网络和反向传播。

这节课的核心内容是：理解并能计算损失函数关于权重的梯度，是设计、训练和理解神经网络的核心能力。下节中，将介绍如何使用链式法则来高效地计算梯度，也就是通常所说的反向传播（backpropagation）机制。该机制能够对包含卷积神经网络在内的几乎所有类型的神经网络的损失函数进行高效的最优化。

此专栏所有文章都是博主辛苦写的，转载请注明出处！
在本专栏全部更新完后，会写一份详细知识点的思维导图，请大家持续关注哈。